Money

Represents a monetary value

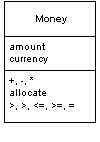
A pretty large proportion of computers in this world manipulate money. As such it's always puzzled me that Money isn't actually a first class data type in any mainstream programming language. That lack of a type causes problems. The most obvious problem surrounds currencies. If all your calculations are done in a single currency, then this isn't a huge problem, but once you involve multiple currencies then you wasn't avoid adding your dollars to your yen without taking the currencies into account. The more subtle problem is with rounding. Monetary calculations are often rounded to the smallest currency unit. When you do this it's easy to lose pennies (or your local equivalent) due to rounding errors.

The good thing about object-oriented programming is that you can fix these problems by creating a Money class that handles these issues. Of course it's still surprising that non of the mainstream base class libraries actually do this

How it Works

The basic idea is to have a Money class with fields for the numeric amount and the currency. You can store the amount as either an integral type or a fixed decimal type. The decimal type is easier for some manipulations and the integral type for others. You should absolutely avoid any kind of floating point type, as that will introduce the kind of rounding problems that Money is intended to avoid. Most of the time people want monetary values rounded to the smallest complete unit, such as cents in the dollar. There are times, however, when fractional money units are needed. It's important to make it clear what kind of money you are working with, especially in an application where you use both kinds. It makes sense to have two different types for the two cases as they behave quite differently under arithmetic.

Money is a Value Object, so it should have its equality and hash code operations overridden to be based on the currency and amount.

Money needs arithmetic operations so that you can use money objects as easily as you use numbers. But arithmetic operations for money have some important differences to money operations in numbers. Most obviously any addition or subtraction needs to be currency aware, so you can react if you try to add together monies of different currencies. The simplest, and most common, response is to treat adding of disparate currencies as an error. In some more sophisticated situations you can use Ward Cunningham's idea of a Money Bag. (A Money Bag is an object that contains monies of multiple currencies together in one object. This object can then participate in calculations just like any money object. You can also value a money bag into a currency.)

Multiplication and division end up being more complicated due to rounding problems. When you multiply money you'll do it with a scalar. If you want to add 5% tax to a bill you multiply by 0.05. So you'll see multiplication by regular numeric types.

The awkward complication comes with rounding, particularly when allocating money between different places. Here's Matt Foemmel's simple conundrum. Suppose I have a business rule that says that I have to allocate the whole amount of a sum of money to two accounts: 70% to one and 30% to another. I have 5 cents to allocate. If I do the math I end up with 3.5 cents and 1.5 cents. Whichever way I round these I get into trouble. If I do the usual rounding to nearest then 1.5 becomes 2 and 3.5 becomes 4. So I end up gaining a penny. Rounding down gives me 4 cents and rounding up gives me six cents. There's no general rounding scheme I can apply to both that will avoid losing or gaining a penny.

I've seen various approaches to this.

Perhaps the most common is to ignore the problem, after all it's only a penny here and there. However this tends to make accountants understandably nervous.
The simplest rule to follow is that when you are allocating you always do the last allocation by subtracting from what you've allocated so far. While this avoids losing pennies you can get a cumulative amount of pennies on the last allocation.
You can allow the users of a money class to declare the rounding scheme when they call the method. This would allow a programmer to say that the 70% case rounds up and the 30% rounds down. This can get more complicated when you are allocating across ten accounts instead of two. You also have to remember to do this. To help encourage people to remember I've seen some money classes force a rounding parameter into the multiply operation. Not just does this force the programmer to think about what rounding they need, it also might remind people about what tests to write. But this gets messy if you have a lot tax calculations that all round the same way.
My favorite solution is to have an allocator function on the Money. The parameter to the allocator is a list of numbers, representing the ratio to be allocated. (so it would look something like aMoney.allocate([7,3])). It then returns a list of monies. The allocator guarantees no pennies get dropped by scattering pennies across the allocated monies in a way that looks pseudo-random from the outside. The allocator is my favorite but has faults: you have to remember to use it and if you have precise rules about where the pennies go they are difficult to enforce.

The fundamental issue here is between using multiplication to determine proportional charge (such as a tax charge) and using multiplication to allocate a sum of money across multiple places. Multiplication works well for the former, but an allocator works better for the latter. The important thing is to consider your intent whenever you want to use multiplication or division on a monetary value.

You may want to convert from one currency to another with a method along the line of aMoney.convertTo(Currency.DOLLARS). The obvious way to do this is to look up an exchange rate and to multiply by it. While this works in many situations, there are cases where it doesn't - again due to rounding. The Euro conversion rules between the fixed Euro currencies had specific roundings applied that made simple multiplication not work. As a result it's wise to have a convertor object to encapsulate the algorithm.

Comparison operations allow you to sort monies. Like the addition operation, conversions need to be currency aware. You can either choose to throw an exception if you compare different currencies, or you can do a conversion.

One of the most useful results of using a money object is that it can encapsulate the printing behavior. This makes it much easier to provide good display on user interfaces and reports. A money class can also parse a string to provide a currency aware input mechanism - which again is very useful for the user interface.

Storing a money in a database always raises a question, since databases also don't seem to understand that money is important (although their vendors do.) The obvious route to take is to use Embedded Value. This results in storing a currency for every money. This can be overkill, for instance an account may have all it's entries be in pounds. In this case you may store the currency on the account and alter the database mapping to pull the account's currency whenever you load entries.

When to Use it

I pretty much use Money for all numeric calculation in object-oriented environments. The primary reason is to encapsulate the handling of rounding behavior, which helps reduce the problems of rounding errors. Another reason to use Money is to make multi-currency work much easier. The most common objection to using Money is performance, although I've only rarely heard of cases where using Money makes any noticeable difference - and even then the encapsulation often makes tuning easier.

Example: A Money Class (Java)

by Matt Foemmel and Martin Fowler

The first decision is what data type to use for the amount. If anyone needs convincing that a floating point number is a bad idea, ask them to run this code.

 
		double val = 0.00;
		for (int i = 0; i < 10; i++) val += 0.10;
		System.out.println(val == 1.00);

With floats safely disposed of, the choice lies between fixed point decimals and integers. In Java this boils down to BigDecimal, BigInteger and long. Using an integral value actually makes the internal math easier, and if we use long we get to use primitives and thus have readable math expressions.

class Money... 
	private long amount;
	private Currency currency;

Since I'm using an integral amount, the integral is the amount of the smallest base unit, which I refer to as cents in the code since that is as good a name as any. By using a long we will get an overflow error if the number gets too big. If you give us $92,233,720,368,547,758.09 we'll write you a version that uses BigInteger.

It's useful to provide constructors from various numeric types

 
	public Money(double amount, Currency currency) {
		this.currency = currency;
		this.amount = Math.round(amount * centFactor());
	}
	public Money(long amount, Currency currency) {
		this.currency = currency;
		this.amount = amount * centFactor();
	}
	private static final int[] cents = new int[] { 1, 10, 100, 1000 };
	private int centFactor() {
		return cents[currency.getDefaultFractionDigits()];
	}

Different currencies have different fractional amounts. Java's 1.4 version has a currency class that will tell you the number of fractional digits in a class. We could determine how many minor units there are in a major unit by raising ten to the power, but that's such a pain to do in Java that the array is easier (and probably quicker). We're prepared to live with the fact that this code breaks if someone uses four fractional digits.

Although most of the time you'll want to use money operation directly, there are occasions when you'll need access to the underlying data

class Money... 
	public BigDecimal amount() {
		return BigDecimal.valueOf(amount, currency.getDefaultFractionDigits());
	}

	public Currency currency() {
		return currency;
	}

You should always question yourself if you find yourself using the accessors, almost always there will be a better way that won't break encapsulation. One example that I couldn't avoid was database mapping, as in Embedded Value

If you use one currency very frequently for literal amounts, then it can be useful to provide a helper constructor.

class Money... 
	public static Money dollars(double amount) {
		return new Money(amount, Currency.USD);
	}

As Money is a Value Object you'll need to define equals..

class Money... 
	public boolean equals(Object other) {
		return (other instanceof Money) && equals((Money)other);
	}
	public boolean equals(Money other) {
		return currency.equals(other.currency) && (amount == other.amount);
	}

And wherever there's an equals there should be a hash

class Money... 
	public int hashCode() {
		return (int) (amount ^ (amount >>> 32));
	}

We'll start going through arithmetic with addition and subtraction.

class Money... 
	public Money add(Money other) {
		assertSameCurrencyAs(other);
		return newMoney(amount + other.amount);
	}
	private void assertSameCurrencyAs(Money arg) {
		Assert.equals("money math mismatch", currency, arg.currency);
	}
	private Money newMoney(long amount) {
		Money money = new Money();
		money.currency = this.currency;
		money.amount = amount;
		return money;
	}

Note the use of a private factory method here that doesn't do the usual conversion into the cent-based amount. We'll use that a few times inside the Money code itself.

With addition defined, subtraction is easy.

class Money... 
	public Money subtract(Money other) {
		assertSameCurrencyAs(other);
		return newMoney(amount - other.amount);
	}

The base method for comparison is compare

class Money... 
	public int compareTo(Object other) {
		return compareTo((Money)other);
	}

	public int compareTo(Money other) {
		assertSameCurrencyAs(other);
		if (amount < other.amount) return -1;
		else if  (amount == other.amount) return 0;
		else return 1;
	}

Although that's all you get on most Java classes these days, we find code is more readable with the others such as these.

class Money... 
	public boolean greaterThan(Money other) {
		return (compareTo(other) > 0);
	}

Now we feel ready to look at multiplication. We're providing a default rounding mode as well as allowing you to set one yourself.

class Money... 
	public Money multiply(double amount) {
		return multiply(new BigDecimal(amount));
	}
	public Money multiply(BigDecimal amount) {
		return multiply(amount, BigDecimal.ROUND_HALF_EVEN);
	}
	public Money multiply(BigDecimal amount, int roundingMode) {
		return new Money(amount().multiply(amount), currency, roundingMode);
	}

If you want to allocate a sum of money amongst many targets, and you don't want to lose cents, then you'll want an allocation method. The simplest one allocates the same amount (almost) amongst a number of targets.

class Money... 
	public Money[] allocate(int n) {
		Money lowResult = newMoney(amount / n);
		Money highResult = newMoney(lowResult.amount + 1);

		Money[] results = new Money[n];
		int remainder = (int) amount % n;
		for (int i = 0; i < remainder; i++) results[i] = highResult;
		for (int i = remainder; i < n; i++) results[i] = lowResult;

		return results;
	}

A more sophisticated allocation algorithm can handle any ratio.

class Money... 
	public Money[] allocate(long[] ratios) {
		long total = 0;
		for (int i = 0; i < ratios.length; i++) total += ratios[i];

		long remainder = amount;
		Money[] results = new Money[ratios.length];
		for (int i = 0; i < results.length; i++) {
			results[i] = newMoney(amount * ratios[i] / total);
			remainder -= results[i].amount;
		}

		for (int i = 0; i < remainder; i++) {
			results[i].amount++;
		}

		return results;
	}

You can use this to solve Foemmel's Conundrum.

class Money... 
	public void testAllocate2() {
		long[] allocation = {3,7};
		Money[] result = Money.dollars(0.05).allocate(allocation);
		assertEquals(Money.dollars(0.02), result[0]);
		assertEquals(Money.dollars(0.03), result[1]);
	}